成品

為什麼要做地球？

回顧原因，它可以應用在很多場景上，例如：行銷網站、企業形象網站、活動網站、全球數位戰情室、航太科技、GIS畫面等等。這些對於前端視覺特效都非常重要。

製作地球也能讓我們釐清貼圖底層的運作模式，不僅討論到底層webGL、fragmentShader、vertexShader的渲染方式，也提到很多種貼圖。

但除了一顆地球在畫面還不夠，仍然需要一點互動，使得地球具有體驗的價值，以及商業上的價值。

實作互動功能

目前為止，我們雖然完成了地球的視覺畫面，但很顯然的，光地球不夠。我們是網頁設計師，用戶應該可以在畫面中互動，才算得上是網頁。否則，一切都只是螢幕保護程式而已。

繼上一篇實作地球之後，我們將提供用戶在各大城市位置中放置圖釘。

使用技術

• 漸變位移——lerp
• 單位向量轉換——normalize
• 用三角函數實作座標轉換——llarToEcef

客戶情境

很多國際設廠的公司會有中控台，以快速釐清各家廠房的運作情況。當然也可能會綜合參數模擬、生產線效率監控、災害告警等。而地球正是中控台印入眼簾的畫面，作為B2B數位孿生的公司，地球的地位相當重要。

而前端的需求大概就是開發類似NASA中控中心的系統，或是全球的子公司/廠房儀表板畫面，使得所有人可以看清楚各地工廠在全球的最新動態。很中二吧？

現今，越來越多中控台從Unity應用程式搖身一變成為網頁的需求。而前端首當其衝就是要把畫面弄得最好，同時還能提供用戶CRUD跟RWD的工具。

以下開發我將聚焦在跳轉畫面，我盡量使用最單純的JS（Vanilla Javascript）示例。

開發鏡頭跳躍功能

開發功能：準備程式碼

我這邊準備好了上一篇的程式碼，我們將沿用。

import * as THREE from 'three';
import { OrbitControls } from 'https://unpkg.com/three@latest/examples/jsm/controls/OrbitControls.js';

const scene = new THREE.Scene();

const camera = new THREE.PerspectiveCamera(50, window.innerWidth / window.innerHeight, 0.1, 1000);
camera.position.set(0, 10, 15)

const renderer = new THREE.WebGLRenderer({ antialias: true });
renderer.setSize(window.innerWidth, window.innerHeight);
document.body.appendChild(renderer.domElement);

// 匯入材質
// image source: https://www.deviantart.com/kirriaa/art/Free-star-sky-HDRI-spherical-map-719281328
const skydomeTexture = new THREE.TextureLoader().load('https://storage.googleapis.com/umas_public_assets/michaelBay/free_star_sky_hdri_spherical_map_by_kirriaa_dbw8p0w%20(1).jpg')
// 帶入材質，設定內外面
const skydomeMaterial = new THREE.MeshBasicMaterial({ map: skydomeTexture, side: THREE.DoubleSide })
const skydomeGeometry = new THREE.SphereGeometry(100, 50, 50)
const skydome = new THREE.Mesh(skydomeGeometry, skydomeMaterial);
scene.add(skydome);

// 新增環境光
const addAmbientLight = () => {
	const light = new THREE.AmbientLight(0xffffff, 0.5)
	scene.add(light)
}

// 新增點光
const addPointLight = () => {
	const pointLight = new THREE.PointLight(0xffffff, 1)
	scene.add(pointLight);
	pointLight.position.set(10, 10, -10)
	pointLight.castShadow = true
	// 新增Helper
	const lightHelper = new THREE.PointLightHelper(pointLight, 5, 0xffff00)
	// scene.add(lightHelper);
	// 更新Helper
	lightHelper.update();
}

// 新增平行光
const addDirectionalLight = () => {
	const directionalLight = new THREE.DirectionalLight(0xffffff, 1)
	directionalLight.position.set(0, 0, 10)
	scene.add(directionalLight);
	directionalLight.castShadow = true
	const d = 10;

	directionalLight.shadow.camera.left = - d;
	directionalLight.shadow.camera.right = d;
	directionalLight.shadow.camera.top = d;
	directionalLight.shadow.camera.bottom = - d;

	// 新增Helper
	const lightHelper = new THREE.DirectionalLightHelper(directionalLight, 5, 0xffff00)
	// scene.add(lightHelper);
	// 更新位置
	directionalLight.target.position.set(0, 0, 0);
	directionalLight.target.updateMatrixWorld();
	// 更新Helper
	lightHelper.update();
}

addPointLight()
addAmbientLight()
addDirectionalLight()

const earthGeometry = new THREE.SphereGeometry(5, 600, 600)
const earthTexture = new THREE.TextureLoader().load('https://storage.googleapis.com/umas_public_assets/michaelBay/day10/8081_earthmap2k.jpg')
// 灰階高度貼圖
const displacementTexture = new THREE.TextureLoader().load('https://storage.googleapis.com/umas_public_assets/michaelBay/day10/editedBump.jpg')
const roughtnessTexture = new THREE.TextureLoader().load('https://storage.googleapis.com/umas_public_assets/michaelBay/day10/8081_earthspec2kReversedLighten.png')
const speculatMapTexture = new THREE.TextureLoader().load('https://storage.googleapis.com/umas_public_assets/michaelBay/day10/8081_earthspec2k.jpg')
const bumpTexture = new THREE.TextureLoader().load('https://storage.googleapis.com/umas_public_assets/michaelBay/day10/8081_earthbump2k.jpg')

const earthMaterial = new THREE.MeshStandardMaterial({
	map: earthTexture,
	side: THREE.DoubleSide,
	roughnessMap: roughtnessTexture,
	roughness: 0.9,
	// 將貼圖貼到材質參數中
	metalnessMap: speculatMapTexture,
	metalness: 1,
	displacementMap: displacementTexture,
	displacementScale: 0.5,
	bumpMap: bumpTexture,
	bumpScale: 0.1,
})
const earth = new THREE.Mesh(earthGeometry, earthMaterial);
scene.add(earth);

const cloudGeometry = new THREE.SphereGeometry(5.4, 60, 60)
// 匯入材質
// texture source: http://planetpixelemporium.com/earth8081.html
const cloudTransparency = new THREE.TextureLoader().load('8081_earthhiresclouds4K.jpg')
// 帶入材質，設定內外面
const cloudMaterial = new THREE.MeshStandardMaterial({
	transparent: true,
	opacity: 1,
	alphaMap: cloudTransparency
})
const cloud = new THREE.Mesh(cloudGeometry, cloudMaterial);
scene.add(cloud);

// 帶入鏡頭跟renderer.domElement實例化它即可
new OrbitControls(camera, renderer.domElement);

const axesHelper = new THREE.AxesHelper(5);
scene.add(axesHelper);

function animate() {
	requestAnimationFrame(animate);
	renderer.render(scene, camera);
	earth.rotation.y += 0.005
	cloud.rotation.y += 0.004
	skydome.rotation.y += 0.001

}
animate();

這是我們上一篇的結果：

我們先把地球自轉的效果移除掉，方便接下來的開發：

function animate() {
	requestAnimationFrame(animate);
	renderer.render(scene, camera);
-	earth.rotation.y += 0.005
	cloud.rotation.y += 0.004
	skydome.rotation.y += 0.001
}

開發功能：準備城市位置

我們假裝正在幫一家公司的海外廠房製作全球中控台好了，廠房位於幾個城市。我就在網路上找到一些城市的經緯度做示範。

我找到這個網站提供很多城市經緯度資料。

網站連結與資料來源

授權方式：Attribution 4.0 International

有了這些資料後，我整理成一份物件清單，作為本次範例中的客戶廠房位址，並放在程式碼中。

const cities = [
	{ name: "Mumbai", id: 1356226629, lat: 19.0758, lon: 72.8775, country: "India" },
	{ name: "Moscow", id: 1643318494, lat: 55.7558, lon: 37.6178, country: "Russia" },
	{ name: "Xiamen", id: 1156212809, lat: 24.4797, lon: 118.0819, country: "China" },
	{ name: "Phnom Penh", id: 1116260534, lat: 11.5696, lon: 104.9210, country: "Cambodia" },
	{ name: "Chicago", id: 1840000494, lat: 41.8373, lon: -87.6862, country: "United States" },
	{ name: "Bridgeport", id: 1840004836, lat: 41.1918, lon: -73.1953, country: "United States" },
	{ name: "Mexico City", id: 1484247881, lat:19.4333, lon: -99.1333 , country: "Mexico" },
	{ name: "Karachi", id: 1586129469, lat:24.8600, lon: 67.0100 , country: "Pakistan" },
	{ name: "London", id: 1826645935, lat:51.5072, lon: -0.1275 , country: "United Kingdom" },
	{ name: "Boston", id: 1840000455, lat:42.3188, lon: -71.0846 , country: "United States" },
	{ name: "Taichung", id: 1158689622, lat:24.1500, lon: 120.6667 , country: "Taiwan" },
]

開發功能：製作圖釘

釘在地球上面的圖釘，我以甜甜圈形狀的物件當作圖釘，目的是避免遮住廠房確切位置。

const geo = new THREE.RingGeometry( 0.1, 0.13, 32 );
const mat = new THREE.MeshBasicMaterial( { color: 0xffff00, side: THREE.DoubleSide } );
const ring = new THREE.Mesh( geo, mat );
scene.add( ring );

它位置會在(0,0,0)，也就是地球裡面，我們暫時看不到它。這是我把地球拿掉時看到的圖釘畫面：

開發功能：製作下拉式選單

我們加上標籤<select> ，設定簡單的樣式跟class name。

<body>
    <main>
			<select style="position:absolute; margin: 10%" class="city-select">       
			</select>
    </main>
</body>

接下來，單向綁定標籤元件，並且渲染選項<option>

// 前面提到的城市資料清單
const cities = [
	// 我們加一個「請選擇」option避免誤導用戶
	{ name: "--- select city ---", id: 0, lat: 0, lon: 0, country: "None" },
	{ name: "Mumbai", id: 1356226629, lat: 19.0758, lon: 72.8775, country: "India" },
	{ name: "Moscow", id: 1643318494, lat: 55.7558, lon: 37.6178, country: "Russia" },
	...
] 
const citySelect = document.getElementsByClassName('city-select')[0]
// 渲染option
citySelect.innerHTML = cities.map( city => `<option value="${city.id}">${city.name}</option>`)

加入傾聽事件，找出城市經緯度：

citySelect.addEventListener( 'change', (event) => {
	const cityId = event.target.value
	const seletedCity = cities.find(city => city.id+'' === cityId)
	console.log(seletedCity)
})

// {name: 'Phnom Penh', id: 1116260534, lat: 11.5696, lon: 104.921, country: 'Cambodia'}

開發功能：經緯度轉換成世界座標

由於我們只知道經緯度座標（Latitude, Longitude, and Altitude，又稱LLA Coordinates），但我們應該要如何將經緯度轉換成世界座標（Earth-centered Earth-fixed，又稱ECEF Coordinates）呢？

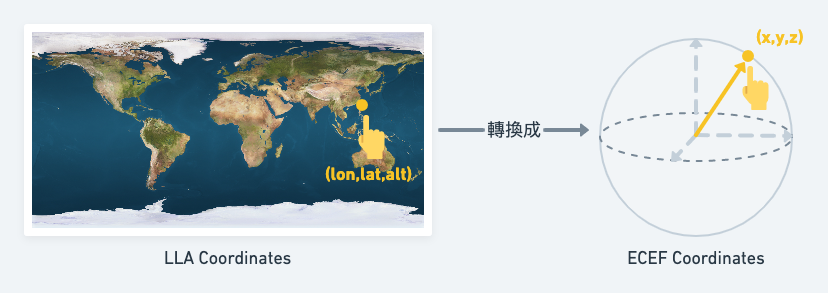
實際上，兩種座標可以透過座標轉換公式求得：

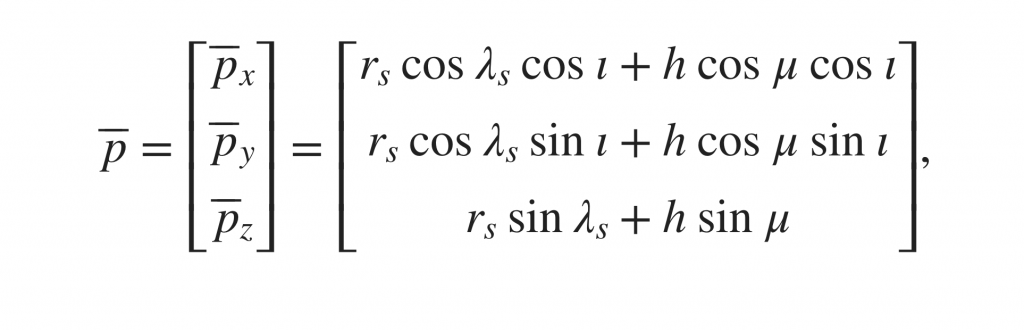
將公式應用在本專案即成為函式：

// 將LLA轉換成ECEF座標
const llaToEcef = (lat, lon, alt, rad) => {
	let f = 0
	let ls = Math.atan((1 - f) ** 2 * Math.tan(lat))
	let x = rad * Math.cos(ls) * Math.cos(lon) + alt * Math.cos(lat) * Math.cos(lon)
	let y = rad * Math.cos(ls) * Math.sin(lon) + alt * Math.cos(lat) * Math.sin(lon)
	let z = rad * Math.sin(ls) + alt * Math.sin(lat)
	return new THREE.Vector3(x, y, z)
}

這個公式是怎麼來的？我們稍候介紹。我們先完成功能。

開發功能：經緯度轉換成弧度

這個函式的帶入參數為弧度，尚不是座標。我們必須要把經緯度轉成弧度，而這又需要另外一個函式幫忙：

const lonLauToRadian = (lon, lat, rad) => llaToEcef(Math.PI * (0 - lat) / 180, Math.PI * (lon / 180), 1, rad)

由於弧度範圍是0~2π，但對於緯度來說範圍是90~-90，也對於經度來說是-180~180的範圍，所以必須將經緯度轉換成弧度。這就是該函式的作用。

開發功能：移動圖釘位置到城市

我們將用戶所選取的城市經緯度帶入上面的函式，即可取得城市在世界座標的位置。

將圖釘位置改成城市位置，並且校正圖釘角度即可。

citySelect.addEventListener( 'change', (event) => {
	const cityId = event.target.value
	const seletedCity = cities.find(city => city.id+'' === cityId)
	// 用前面的函式所取得的座標
	const cityEciPosition = lonLauToRadian(seletedCity.lon, seletedCity.lat, 4.4)
	// 指定位置給圖釘
	ring.position.set(cityEciPosition.x, -cityEciPosition.z, -cityEciPosition.y)	
	// 圖釘永遠都看像世界中心，所以不會歪斜。
	ring.lookAt(center)
})

• 補充一下：在介紹OrbitControl時，有提到不要用lookAt()控制鏡頭。這是因為OrbitControl是鏡頭方向的代理人，如果直接透過lookAt()控制鏡頭將使得控制鏡頭方向的代理人OrbitControl與lookAt()的操作衝突。然而lookAt()仍然是控制物件（鏡頭以外的物件）其角度很好的函式，我們在這裡使用它控制圖釘的角度。

完成品

我們看看目前的成品：

可以看到，圖釘已經定位在城市位置了。

接下來，無論用戶如何切換，我們都可以找出城市的位置，這還多虧了LLA轉換成ECEF座標的函式。

這樣就完成了！

經緯度轉三維空間座標

在進入下一篇之前，我們需要先釐清一下LLA轉換成ECEF座標的函式。

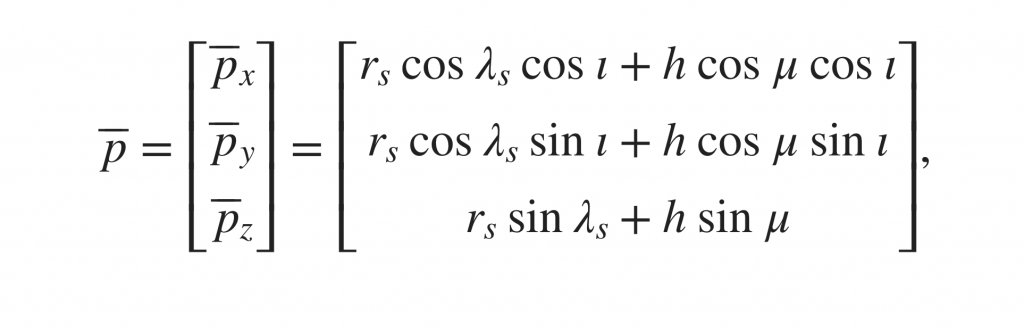
這個函式看似複雜，其就跟矩陣那篇所提到的旋轉函式有異曲同工之妙。

// 給定旋轉之前的座標
let x
let y
// 給定旋轉角度
let θ
// ax,ay為旋轉的結果
const ax = x * cos(θ) + y * sin(θ)
const ay = x * -sin(θ) + y * cos(θ)

座標：經緯度轉三維空間座標原理

球座標的轉換到底是怎麼來？我從MathWorks找到這個函式。下面介紹原理：

圖片來源

座標：球座標轉換

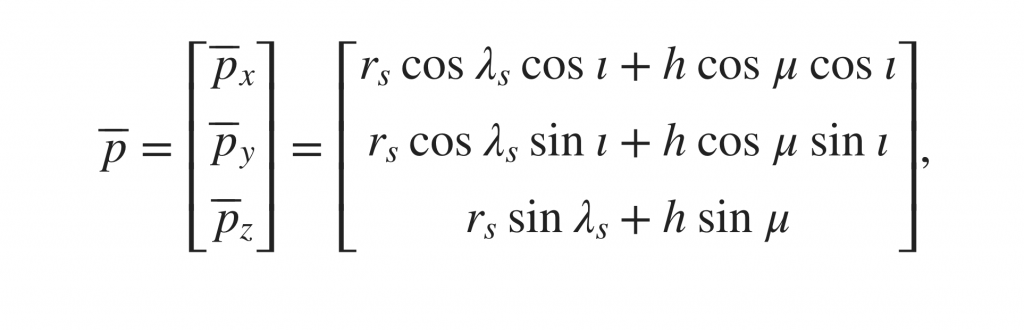
首先，我們的任務就是將經緯度座標變成三維空間座標。

經緯度就是以地圖中心(0,0)水平旋轉、垂直旋轉的位置描述方式。

例如桃園外海座標(東經121 ,北緯25)即是經度0度向東移動121度，北緯25即是赤道向北移動25度。我們可以得知——一切都是角度。

也就是說，可以把經度跟緯度想像成旋轉角度。如果我們有水平旋轉角度跟垂直旋轉角度，再加上地球半徑，就可以用公式求得三維座標了。

下面是一個三維空間，如果p是地球半徑，則我們可以透過上面的概念，旋轉φ以及θ來求得(x,y,z)座標。而這就如同我們從經緯度找到桃園外海座標在三維空間的座標位置一樣。θ為Y軸的旋轉角度，就如同經度是描述Y軸的旋轉角度一樣，而φ則如同緯度描述旋轉角度一樣。

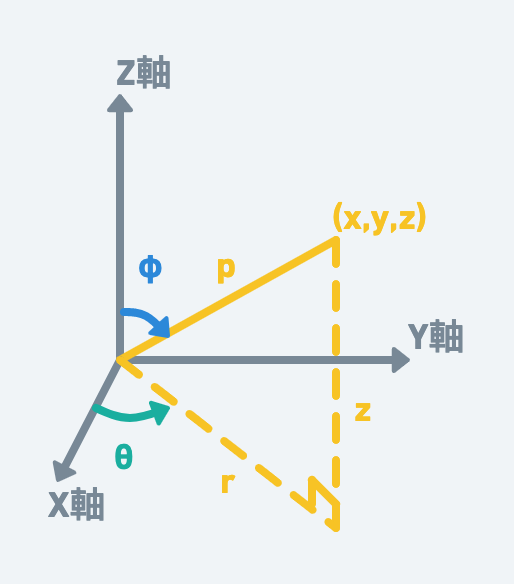
在這張圖可以看到，z垂直於xy平面。

為了更好理解，我們把畫面切到線段z跟r的剖面好了：

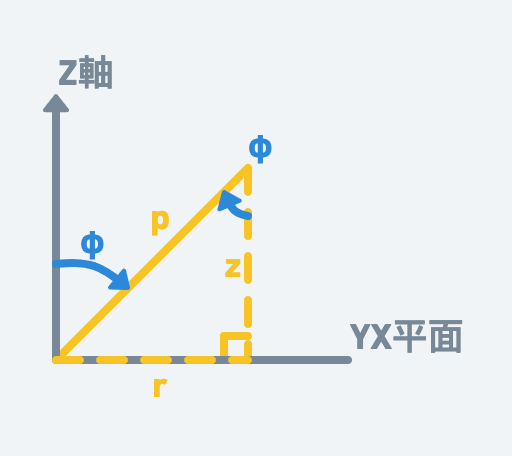
根據三角函數，我們得知：

// 下面這行z算出來是自己
z = p*(z/p)
// z/p乃φ斜邊分之鄰邊，以cos(φ)代替z/p
z = ρ*cos(φ)
// 下面這行r算出來是自己
r = ρ*(r/p)
// r/p乃φ斜邊分之對邊，以sin(φ)代替r/p
r = ρ*sin(φ)

我們先記住這個結果，現在先繼續把視角轉到XY的平面看這個座標：

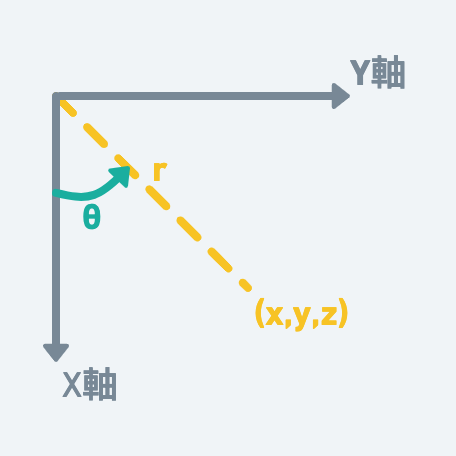
為求方便，我加兩條輔助線：

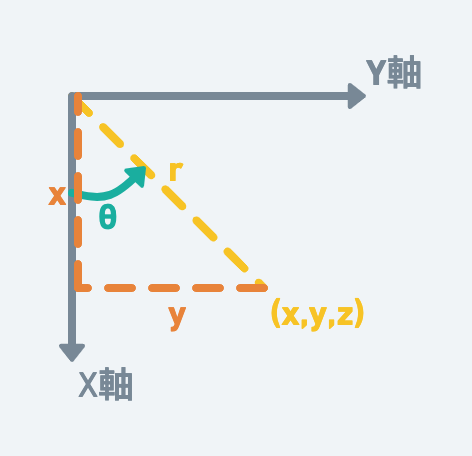
同樣用三角函數，可以推算(x,y,z)中x,y的位置：

// 下面這行x算出來是自己
x = r*(x/r)
// x/r乃θ斜邊分之鄰邊，以cos(θ)代替x/r
x = r*cos(θ)
// 下面這行r算出來是自己
y = r*(y/r)
// y/r乃θ斜邊分之對邊，以sin(θ)代替y/r
y = r*sin(θ)

現在，我們有兩個等式

x = r*cos(θ)
y = r*sin(θ)

還記得剛剛我們所記住的結果嗎？r 我們早就算出來了，我們把r放在等式裡面

x = ρ*sin(φ)*cos(θ)
y = ρ*sin(φ)*sin(θ)

然後再加上我們也早就求出來的z，就變成：

x = ρ*sin(φ)*cos(θ)
y = ρ*sin(φ)*sin(θ)
z = ρ*cos(φ)

於是，只要我們知道從z軸到p的角度φ，以及x到p的角度θ，就可以得到(x,y,z)座標。

座標：經緯度與地球座標轉換

使用上面這個概念，我們就能找到經緯度在笛卡兒三維座標的位置。因為經緯度也像φ、θ一樣，是表達角度的方式。

但困難的是：

1. 地球不是完整的圓，而是橢圓形的
2. 地表有海拔高度，這使得計算起來沒辦法把(x,y,z)位置完美的落在地表。

但沒關係，數學家仍然算得出來，並克服了上面這兩個難題，使得我們有公式可以用。

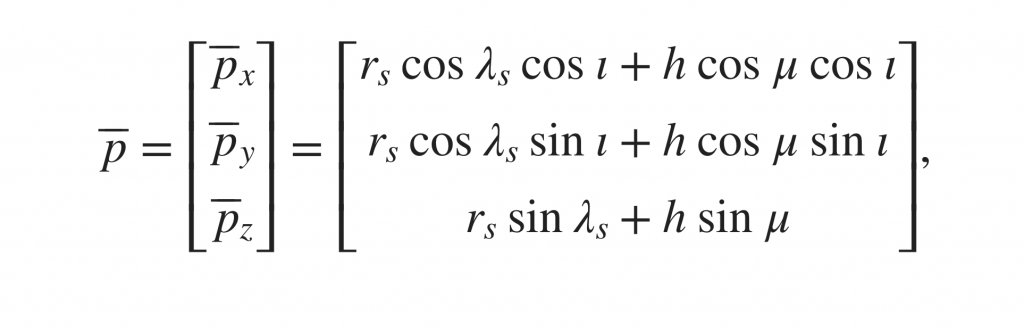
這個公式裡面，h就代表海拔高度的計算，使得問題二有了解套方式。

至於橢圓形的問題，也有了公式帶入。你如果仔細看可以看見：圖中的公式怎麼三角函數順序，跟我剛才推導的結果不一樣。

這是因為橢圓形的計算比較複雜不好解釋，這個網站提供了公式給大家參考。

https://www.mathworks.com/help/aeroblks/llatoecefposition.html

有興趣了可以深入理解，我這邊不多作解釋，因為會太離題。總之用球座標的概念，再考量到橢圓形、高度之後，就能取得剛剛開發時所用的函式：

// 將LLA轉換成ECEF座標
const llaToEcef = (lat, lon, alt, rad) => {
	let f = 0
	let ls = Math.atan((1 - f) ** 2 * Math.tan(lat))
	// alt主要為海拔高度以上的位置計算。本專案需求帶入0即可。但仍保留程式碼示例。
	let x = rad * Math.cos(ls) * Math.cos(lon) + alt * Math.cos(lat) * Math.cos(lon)
	let y = rad * Math.cos(ls) * Math.sin(lon) + alt * Math.cos(lat) * Math.sin(lon)
	let z = rad * Math.sin(ls) + alt * Math.sin(lat)
	return new THREE.Vector3(x, y, z)
}

你會發現：有些開發上我們會引用很多公式，然後小小修改一下。如果不懂得常用的數學，那麼小小修改也會很花功夫。我這邊還是先聚焦在比較簡單的推導上，而這已經滿足很大的開發需求了。

CodePen

https://codepen.io/umas-sunavan/pen/NWMXYwZ

下篇

本篇我們建立了圖釘，並且讓圖釘透過座標轉換的公式被放在正確的位置上。

下篇我將介紹透過投影/反投影，藉此讓我們可以在地球上看到各個城市的名稱。

除此之外，我們也需要讓鏡頭移動到城市的位置，而這個會需要用到lerp，跟normalize去調整鏡頭移動的方式，而這兩個也算是當時在討論向量時提到的有用函式，下篇將實際應用它。

下一篇我們將介紹鏡頭在各大城市之間的移動

參考資料

LLA to ECEF Position

球座標計算

球座標計算問題討論

球座標問題討論2

球座標轉換的python函式